Advertisements (Quảng cáo)
Hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều dài 1m. Tính góc \(\alpha = \widehat {DAB} = \widehat {CBA}\) sao cho hình thang có diện tích lớn nhất và diện tích lớn nhất đó (h.1.1)
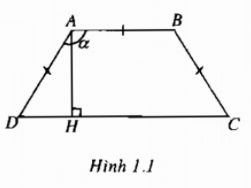
Giải
Dựng \(AH \bot CD\). Đặt \(x = \widehat {ADC,}0 < x < {\pi \over 2}\) , ta được AH = sinx; DH = cosx; DC = 1+ 2cosx. Diện tích hình thang là
\(S = {{AB + CD} \over 2}AH = (1 + \cos x)sinx;0 < x < {\pi \over 2}\)
Bài toán quy về: Tìm \(x \in \left( {0;{\pi \over 2}} \right)\) sao cho tại điểm đó s đạt giá trị lớn nhất trên khoảng \(\left( {0;{\pi \over 2}} \right)\)
\(S ‘= (\cos x + 1)(2\cos x – 1);0 < x < {\pi \over 2}\)
Hình thang có diện tích lớn nhất khi \(\alpha = {{2\pi } \over 3}\) . Khi đó diện tích hình thang là \(S = {{3\sqrt 3 } \over 4}({m^2})\)