Chứng minh rằng hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hướng dẫn làm bài:
Hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Không có đạo hàm tại x = 0 vì:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2 \cr
& \mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2 \cr} \)
Mặt khác, với x < 0 thì \(y’ = {1 \over 2}\cos {x \over 2}\) , với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
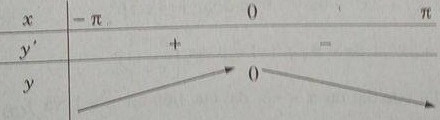
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 0.
