Tìm các khoảng đồng biến, nghịch biến của các hàm số:
a) \(y = {{3 - 2x} \over {x + 7}}\)
b) \(y = {1 \over {{{(x - 5)}^2}}}\)
c) \(y = {{2x} \over {{x^2} - 9}}\)
d) \(y = {{{x^4} + 48} \over x}\)
e) \(y = {{{x^2} - 2x + 3} \over {x + 1}}\)
g) \(y = {{{x^2} - 5x + 3} \over {x - 2}}\)
Hướng dẫn làm bài
a) TXĐ: R\ {-7}
\(y’ = {{ - 17} \over {{{(x + 7)}^2}}}\)
y’ < 0 trên các khoảng (-∞; -7), (-7; +∞) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R\ {5}
\(y’ = {{ - 2} \over {{{(x - 5)}^3}}}\)
y’ < 0 trên khoảng (5; +∞) nên y nghịch biến trên khoảng (5; +∞)
y’ > 0 trên khoảng (-∞; 5) nên y đồng biến trên khoảng (-∞; 5)
c) TXĐ: R\{-3; 3}
\(y’ = {{ - 2({x^2} + 9)} \over {{{({x^2} - 9)}^2}}}\)
Advertisements (Quảng cáo)
y’ < 0 trên các khoảng (-∞; - 3), (-3; 3), (3; +∞) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R\ {0}
\(y’ = {{3({x^4} - 16)} \over {{x^2}}} = {{3({x^2} - 4)({x^2} + 4)} \over {{x^2}}}\)
y’ = 0 <=> \(\left[ {\matrix{{x = - 2} \cr {x = 2} \cr} } \right.\)
Bảng biến thiên:
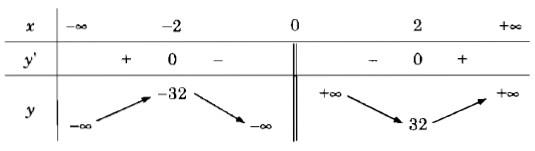
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
\(y’ = {{{x^2} + 2x - 5} \over {{{(x + 1)}^2}}}\)
y’ = 0 <=> \(\left[ {\matrix{{x = - 1 - \sqrt 6 } \cr {x = - 1 + \sqrt 6 } \cr} } \right.\)
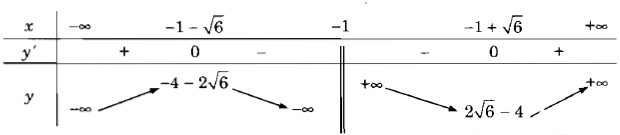
Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6 ),( - 1 + \sqrt 6 ; + \infty )\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1),( - 1; - 1 + \sqrt 6 )\)
g) TXĐ: R\ {2}
\(y’ = {{{x^2} - 4x + 7} \over {{{(x - 2)}^2}}} > 0\)
(do \({x^2} - 4x + 7\) có ∆’ = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ;2),(2; + \infty )\)
