Xét tính đơn điệu của các hàm số:
a) \(y = \sqrt {25 - {x^2}} \)
b) \(y = {{\sqrt x } \over {x + 100}}\)
c) \(y = {x \over {\sqrt {16 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Hướng dẫn làm bài
a) TXĐ: [-5; 5]
\(y’ = {{ - x} \over {\sqrt {25 - {x^2}} }}\) ; y’ = 0 <=> x = 0
Bảng biến thiên:
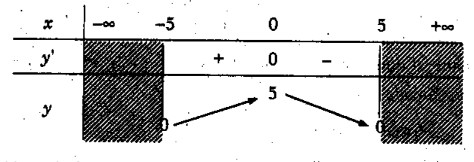
Vậy hàm số đồng biến trên khoảng (-5; 0) nghịch biến trên khoảng (0; 5)
Advertisements (Quảng cáo)
b) TXĐ: [0; +∞)
\(y’ = {{100 - x} \over {2\sqrt x {{(x + 100)}^2}}}\) ; y’ = 0 <=> x = 100
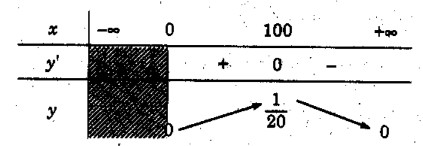
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; +∞)
c) TXĐ: (-4; 4)
\(y’ = {{16} \over {(16 - {x^2})\sqrt {16 - {x^2}} }} > 0\) ; ∀ x ∈ (-4; 4).
Vậy hàm số đồng biến trên khoảng (-4; 4).
d) TXĐ: (-∞; \(\sqrt 6 \)) ∪ (\(\sqrt 6 \); +∞)
\(y’ = {{2{x^2}({x^2} - 9)} \over {({x^2} - 6)\sqrt {{x^2} - 6} }}\) ; y’ = 0 <=> x = ±3
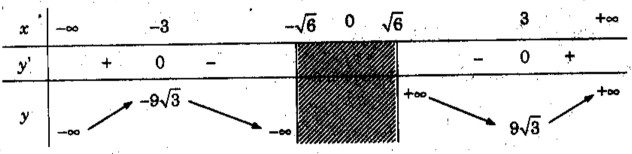
Vậy hàm số đồng biến trên các khoảng (-∞; -3), (3; +∞), nghịch biến trên các khoảng (-3;\(-\sqrt 6 \) ), (\(\sqrt 6 \); 3).
