Advertisements (Quảng cáo)
Cho hàm số : \(y = {1 \over 4}{x^3} – {3 \over 2}{x^2} + 5\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho
b) Tìm các giá trị của tham số m để phương trình x3 – 6x2 + m = 0 có 3 nghiệm thực phân biệt.
Hướng dẫn làm bài:
a) Tập xác định: D = R; \(y’ = {3 \over 4}{x^2} – 3x\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 4 \hfill \cr} \right.\)
Hàm số đồng biến trên mỗi khoảng \(( – \infty ;0),(4; + \infty )\).
Hàm số nghịch biến trên mỗi khoảng (0; 4).
Hàm số đật cực đại tại x = 0, yCĐ = 5. Hàm số đạt cực tiểu tại x = 4, yCT = -3.
Advertisements (Quảng cáo)
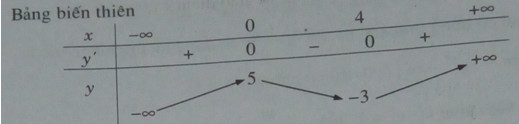
Đồ thị đi qua A(-2; -3); B(6; 5).
b)
\(\eqalign{
& {x^3} – 6{x^2} + m = 0 \cr
& \Leftrightarrow {x^3} – 6{x^2} = – m \cr} \) (1)
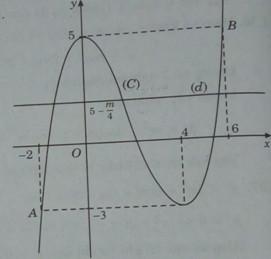
\( \Leftrightarrow {1 \over 4}{x^3} – {3 \over 2}{x^2} + 5 = 5 – {m \over 4}\)
Số nghiệm thực phân biệt của phương trình (1) bằng số giao điểm phân biệt của đồ thị (C) và đường thẳng (d): \(y = 5 – {m \over 4}\)
Suy ra (1) có 3 nghiệm thực phân biệt khi và chỉ khi: \( – 3 < 5 – {m \over 4} < 5 \Leftrightarrow 0 < m < 32\)