Biện luận theo k số nghiệm của phương trình:
a) \({(x - 1)^2} = 2|x - k|\)
b) \({(x + 1)^2}(2 - x) = k\)
Hướng dẫn làm bài:
a) Phương trình đã cho tương đương với phương trình:
\(2(x - k) = \pm {(x - 1)^2}\)
\( \Leftrightarrow \left[ {\matrix{{ - {x^2} + 4x - 1 = 2k} \cr {{x^2} + 1 = 2k} \cr} } \right.\)
Ta vẽ đồ thị của hai hàm số: \(y = - {x^2} + 4x - 1\) và \(y = {x^2} + 1\)
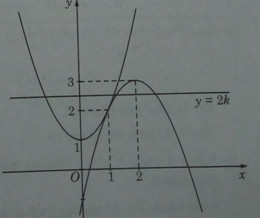
Từ đồ thị ta suy ra:
2k > 3 : phương trình có hai nghiệm;
2k = 3 : phương trình có ba nghiệm;
2 < 2k < 3 : phương trình có bốn nghiệm;
2k = 2 : phương trình có ba nghiệm;
1 < 2k < 2 : phương trình có bốn nghiệm ;
2k = 1 : phương trình có ba nghiệm ;
Advertisements (Quảng cáo)
2k < 1 : phương trình có hai nghiệm.
\(\Leftrightarrow \left[ {\matrix{
{1 < k < {3 \over 2},{\rm{or}}{1 \over 2} < k < 1(1)} \cr
{k = 1,\,\,{\rm{hoặc }}\,\,\,k = {1 \over 2},\,\,{\rm{hoặc }}\,\,\,k = {3 \over 2}(2)} \cr
{k > {3 \over 2},\,\,{\rm{hoặc }}\,\,\,k < {1 \over 2}(3)} \cr} } \right.\)
(1) : phương trình có bốn nghiệm;
(2): phương trình có ba nghiệm ;
(3): phương trình có hai nghiệm.
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {(x + 1)^2}(2 - x)\) .
\(y = - {x^3} + 3x + 2 \Rightarrow y’ = - 3{x^2} + 3\)
\(y’ = 0 \Leftrightarrow \left[ {\matrix{
{x = 1} \cr
{x = - 1} \cr} } \right.\)
Bảng biến thiên:
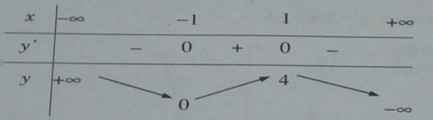
Đồ thị:
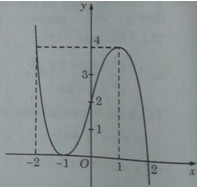
Từ đồ thị hàm số ta suy ra:
* k > 4 hoặc k < 0: phương trình có một nghiệm;
* k = 4 hoặc k = 0 : phương trình có hai nghiệm;
* 0 < k < 4: phương trình có ba nghiệm.
