Câu hỏi 4 trang 36 Giải tích 12: Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x4+ 2×2 + 3....

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x⁴+ 2x² + 3.

Bằng đồ thị, biện luận theo m số nghiệm của phương trình -x⁴+ 2x² + 3 = m

1.TXĐ: D = R.

2. Sự biến thiên:

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = – \infty \cr
& \mathop {\lim }\limits_{x \to – \infty } y = – \infty \cr} \)

y’= -4x³ + 4x. Cho y’ = 0 ⇒ x = 0 hoặc x = ±1.

Bảng biến thiên

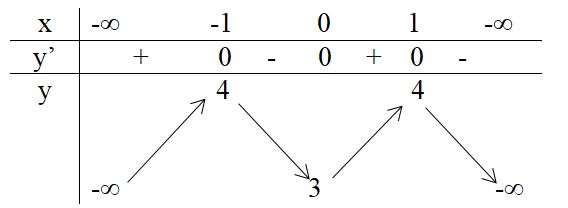
Hàm số đồng biến trên: (-∞,-1), (0,1).

Hàm số nghịch biến trên: (-1,0), (1, +∞).

Hàm số đạt cực đại bằng 4 tại x = -1 và x = 1.

Hàm số đạt cực tiểu bằng 3 tại x = 0.

Đồ thị

Giải biện luận phương trình -x⁴+ 2x² + 3 = m

Số giao điểm của hai đồ thị y =  -x⁴+ 2x² + 3 và y = m là số nghiệm của phương trình trên.

Với m > 4. Hai đồ thị không giao nhau nên phương trình vô nghiệm.

Với m = 4 và m < 3. Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt.

Với m = 3. Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt.

Với 3 < m < 4. Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt.