a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: \(y = - {x^3} + 3x + 1\)
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàm số: \(y = {(x + 1)^3} - 3x - 4\)
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình: \({(x + 1)^3} = 3x + m\)
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng \(y = - {x \over 9} + 1\)
Hướng dẫn làm bài:
a)
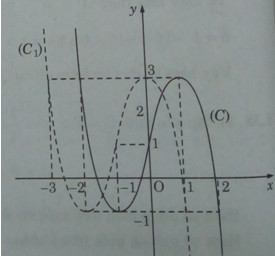
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
\(y = f(x) = - {(x + 1)^3} + 3(x + 1) + 1\) hay \(f(x) = - {(x + 1)^3} + 3x + 4\) (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số \(y = g(x) = {(x + 1)^3} - 3x - 4\)
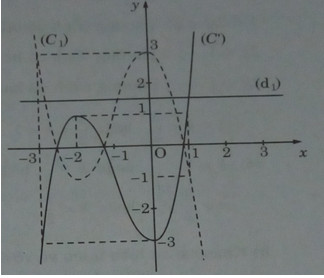
c) Ta có: \({(x + 1)^3} = 3x + m\) (1)
\( \Leftrightarrow {(x + 1)^3} - 3x - 4 = m - 4\)
Advertisements (Quảng cáo)
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
\(y = g(x) = {(x + 1)^3} - 3x - 4\) (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng \(y = - {x \over 9} + 1\) nên ta có hệ số góc bằng 9.
Ta có: \(g'(x) = 3{(x + 1)^2} - 3\)
\(g'(x) = 9 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 3 \hfill \cr} \right.\)
Có hai tiếp tuyến phải tìm là:
\(y – 1 = 9(x – 1) ⇔ y = 9x – 8\);
\(y + 3 = 9(x + 3) ⇔ y = 9x + 24.\)
