Từ đồ thị của hàm số \(y = {\log _4}x\) , hãy vẽ đồ thị của các hàm số sau:
a) \(y = |{\log _4}x|\)
b) \(y = {\log _4}|x|\)
c) \(y = {\log _4}x + 2\)
d) \(y = 1 - {\log _4}x\)
Hướng dẫn làm bài:
a)
\(y = |{\log _4}x| = \left\{ {\begin{array}{*{20}{c}}
{{{\log }_4}x,\,\,khi\,\,x \ge 1}\\
{ - {{\log }_4}x,\,\,khi\,\,0 < x < 1}
\end{array}} \right.\)
Do đó, đồ thị của hàm số \(y = |{\log _4}x|\) gồm:
- Phần đồ thị của hàm số \(y = {\log _4}x\) ứng với \(x \ge 1\)
- Phần đối xứng qua trục hoành của đồ thị hàm số \(y = {\log _4}x\) ứng với 0 < x < 1.
Vậy đồ thị có dạng như Hình 53.
Advertisements (Quảng cáo)
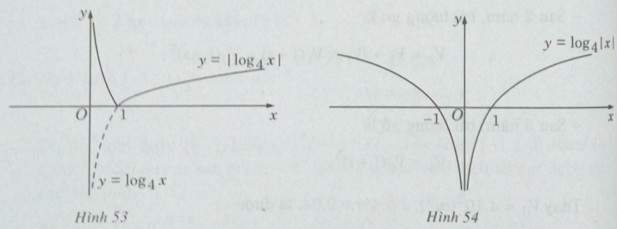
b) Hàm số \(y = {\log _4}|x|\) có tập xác định D = R\{0} và là hàm số chẵn vì:
\(y( - x) = {\log _4}| - x| = {\log _4}|x| = y(x)\)
Do đó, đồ thị của hàm số này có trục đối xứng là trục tung, trong đó phần đồ thị ứng với x > 0 là đồ thị của hàm số \(y = {\log _4}x\)
Vậy ta có đồ thị như Hình 54.
c) Đồ thị của hàm số nhận được từ đồ thị của hàm số bằng phép tịnh tiến song song với trục tung lên trên 2 đơn vị (H.55)

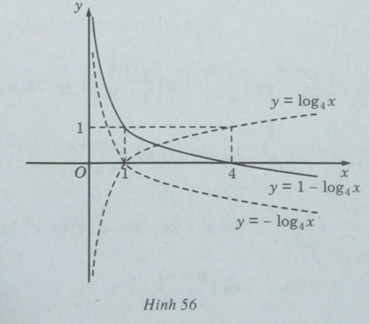
d) Để vẽ đồ thị của hàm số \(y = 1 - {\log _4}x\) , ta thực hiện các bước sau:
- Lấy đối xứng qua trục hoành đồ thị của hàm số \(y = {\log _4}x\) để được đồ thị của hàm số \(y = - {\log _4}x\) ;
- Tịnh tiến song song với trục tung đồ thị của hàm số \(y = - {\log _4}x\) lên phía trên 1đơn vị.
Vậy ta có đồ thị của hàm số \(y = 1 - {\log _4}\) như trên Hình 56.