Giải các bất phương trình sau bằng đồ thị:
a) \({(\frac{1}{2})^x} < x - \frac{1}{2}\)
b) \({(\frac{1}{3})^x} \ge x + 1\)
c) \({\log _{\frac{1}{3}}}x > 3x\)
d) \({\log _2}x \le 6 - x\)
Hướng dẫn làm bài:
a) Vẽ đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) và đường thẳng \(y = x - \frac{1}{2}\) trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) nằm phía dưới đường thẳng \(y = x - \frac{1}{2}\) . Vậy tập nghiệm của bất phương trình đã cho là \((1; + \infty )\)
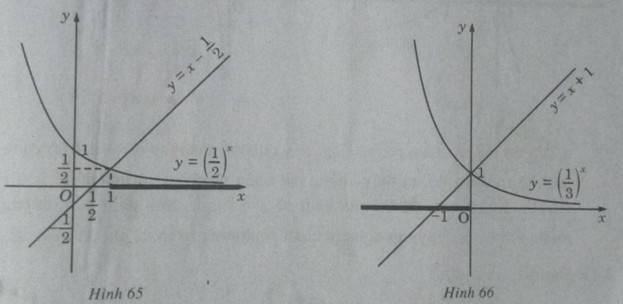
b) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Advertisements (Quảng cáo)
Khi x < 0 đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;0]\)
c) Vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\) (H.67)
Khi \(x < \frac{1}{3}\) đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;\frac{1}{3})\) .
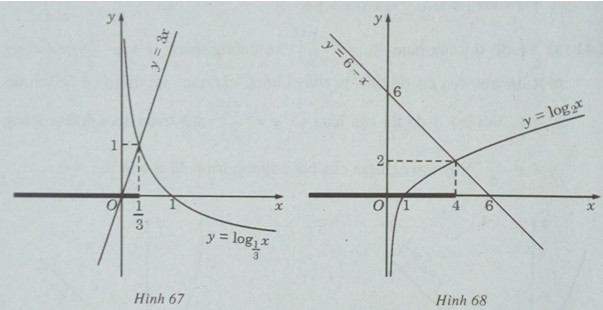
d) Vẽ đồ thị của hàm số \(y = {\log _2}x\) và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
Khi x < 4, đồ thị của hàm số \(y = {\log _2}x\) nằm phía dưới y = 6 – x .
Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;4]\).
