Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng . Bài 3.36 trang 130 sách bài tập (SBT) – Hình học 12 - Bài 3. Phương trình đường thẳng
Tính khoảng cách từ điểm A(1; 0; 1) đến đường thẳng \(\Delta :{{x - 1} \over 2} = {y \over 2} = {z \over 1}\)
Hướng dẫn làm bài:
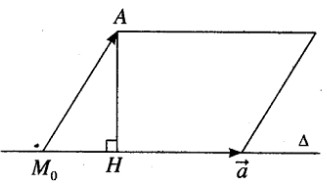
Đường thẳng \(\Delta \) đi qua điểm M0(1; 0; 0) và có vecto chỉ phương \(\overrightarrow a = (2;2;1)\) .
Advertisements (Quảng cáo)
Ta có \(\overrightarrow {{M_0}A} = (0;0;1),\overrightarrow n = \overrightarrow a \wedge \overrightarrow {{M_0}A} = (2; - 2;0)\) .
\(d(A,\Delta ) = {{|\overrightarrow n |} \over {|\overrightarrow a |}} = {{\sqrt {4 + 4 + 0} } \over {\sqrt {4 + 4 + 1} }} = {{2\sqrt 2 } \over 3}\)
Vậy khoảng cách từ điểm A đến \(\Delta \) là \({{2\sqrt 2 } \over 3}\).