Cho hai đường thẳng \(\Delta :{{x - 1} \over 2} = {{y + 3} \over 1} = {{z - 4} \over { - 2}}\)
\(\Delta ‘:{{x + 2} \over { - 4}} = {{y - 1} \over { - 2}} = {{z + 1} \over 4}\)
a) Xét vị trí tương đối giữa \(\Delta \) và \(\Delta ‘\) ;
b) Tính khoảng cách giữa \(\Delta \) và \(\Delta ‘\) .
Hướng dẫn làm bài:
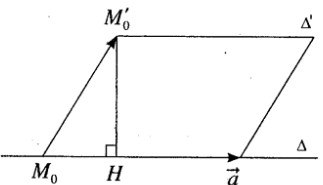
a) \(\Delta \) đi qua điểm M0(1; -3; 4) và có vecto chỉ phương \(\overrightarrow a = (2;1; - 2)\)
Advertisements (Quảng cáo)
\(\Delta ‘\) đi qua điểm M0’ (-2; 1; -1) và có vecto chỉ phương \(\overrightarrow {a’} = ( - 4; - 2;4)\)
Ta có \(\left\{ {\matrix{{\overrightarrow {a’} = 2\overrightarrow a } \cr {{M_0} \notin \Delta ‘} \cr} } \right.\)
Vậy \(\Delta ‘\) song song với \(\Delta \)
b) Ta có \(\overrightarrow {{M_0}M{‘_0}} = ( - 3;4; - 5)\)
\(\overrightarrow a = (2;1; - 2)\)
\(\overrightarrow n = \overrightarrow {{M_0}M{‘_0}} \wedge \overrightarrow a = ( - 3; - 16; - 11)\)
\(d(\Delta ,\Delta ‘) = M{‘_0}H = {{|\overrightarrow n |} \over {|\overrightarrow a |}} = {{\sqrt {9 + 256 + 121} } \over {\sqrt {4 + 1 + 4} }} = {{\sqrt {386} } \over 3}\)
