Cho hai đường thẳng : \(d:{{x - 1} \over { - 1}} = {{y - 2} \over 2} = {z \over 3}\) và \(d’:\left\{ {\matrix{{x = 1 + t’} \cr {y = 3 - 2t’} \cr {z = 1} \cr} } \right.\)
Lập phương trình đường vuông góc chung của d và d’.
Hướng dẫn làm bài:
Phương trình tham số của đường thẳng d:\(\left\{ {\matrix{{x = 1 - t} \cr {y = 2 + 2t} \cr {z = 3t} \cr} } \right.\)
Vecto chỉ phương của hai đường thẳng d và d’lần lượt là \(\overrightarrow a = ( - 1;2;3),\overrightarrow {a’} = (1; - 2;0)\).
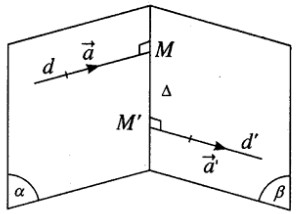
Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’ ; 1) trên d’ ta có \(\overrightarrow {MM’} = (t’ + t;1 - 2t’ - 2t;1 - 3t)\) .
MM’ là đường vuông góc chung của d và d’.
Advertisements (Quảng cáo)
\(\Leftrightarrow \left\{ {\matrix{{\overrightarrow {MM’} .\overrightarrow a = 0} \cr {\overrightarrow {MM’} .\overrightarrow {a’} = 0} \cr} } \right.\)
\(\Leftrightarrow \left\{ {\matrix{{ - t’ - t + 2 - 4t’ - 4t + 3 - 9t = 0} \cr {t’ + t - 2 + 4t’ + 4t = 0} \cr} } \right.\)
\( \Leftrightarrow \left\{ {\matrix{{5t’ + 14t = 5} \cr {5t’ + 5t = 2} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{t = {1 \over 3}} \cr {t’ = {1 \over {15}}} \cr} } \right.\)
Thay giá trị của t và t’ vào ta được tọa độ M và M’ là \(M({2 \over 3};{8 \over 3};1),M'({{16} \over {15}};{{43} \over {15}};1)\)
Do đó \(\overrightarrow {MM’} = ({6 \over {15}};{3 \over {15}};0)\)
Suy ra đường vuông góc chung \(\Delta \) của d và d’ có vecto chỉ phương \(\overrightarrow u = (2;1;0)\)
Vậy phương trình tham số của \(\Delta \) là: \(\left\{ {\matrix{{x = {2 \over 3} + 2t} \cr {y = {8 \over 3} + t} \cr {z = 1} \cr} } \right.\)
