Thiết lập phương trình động lực học và tính tần số góc của dao động tự do của các hệ dao động sau đây :
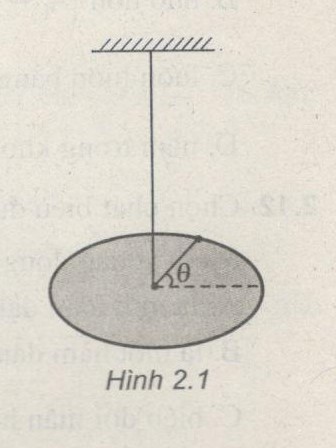
a) Con lắc xoắn : một vật nặng treo ở đầu một sợi dây thẳng đứng đi qua trọng tâm của vật. I momen quán tính của vật đối với trục là sợi dây . Hằng số xoắn của sợi dây là C : khi C bị xoắn một góc \(\theta \) thì momen xoắn là \( - C\theta \) (Hình 2.1)
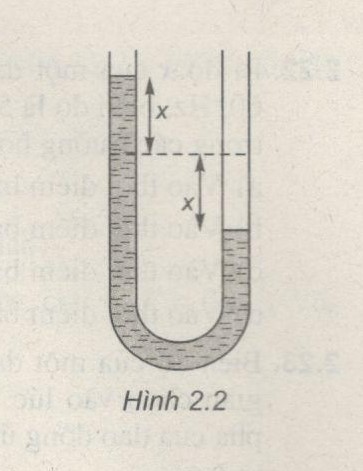
b) Chất lỏng khối lượng riêng \(\rho \) chứa trong một bình chữ U có tiết diện không đổi và bằng S, bỏ qua ma sát (Hình 2.2)
Tính kết quả bằng số, biết rằng chất lỏng là thủy ngân có khối lượng riêng \(\rho = 13,6\,\,g/c{m^3}\). Bình có tiết diện \(S = 0,3\,\,c{m^2}\) và chứa 121 g thủy ngân.

a) Phương trình động lực học :
Momen lực tác dụng = (Momen quán tính)\( \times \) (gia tốc góc)
\( - C\theta = I\theta ”\)
Hay là \(\theta ” + {C \over I}\theta = 0\)
Đây là phương trình động lực học của dao động điều hòa với tần số góc :
\(\omega = \sqrt {{C \over I}} \)
Advertisements (Quảng cáo)
Phương trình dao động là :
\(\theta = {\theta _0}\cos \left( {\omega t + \varphi } \right)\)
Phương trình này đúng cả khi góc \(\theta \) không phải là nhỏ.
b) Khi cân bằng, mực chất lỏng ở hai nhánh của ống hình chữ U bằng nhau. Khi có độ chênh lệch là \(x\) (li độ) của mức chất lỏng trong một nhánh so với mức chất lỏng lúc cân bằng, thì độ chênh mức trong hai nhánh là 2x.
Lực tác dụng lên cả khối chất lỏng trong ống chữ U là :
\(F = - 2xS\rho g = - 2S\rho gx\)
Lực này tỉ lệ với li độ \(x\) và tạo nên dao dộng của cả khối chất lỏng m chứa trong ống chữ U. Phương trình động lực học :
\( - 2S\rho gx = mx”\)
Hay là : \(x” + {{2S\rho g} \over m}x = 0\)
Tần số góc của dao động là : \(\omega = \sqrt {{{2S\rho g} \over m}} \)
Áp dụng bằng số : \(\omega = \sqrt {{{2.0,00003.13600.9,81} \over {0,121}}} \approx 8,1\,\,\,rad/s\)
(Chu kì T = 0,77 s).
