Giải mục 2 trang 10, 11, 12 Toán 12 tập 1 - Chân trời sáng tạo: Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với...

Khám phá2

Trả lời câu hỏi Khám phá 2 trang 10

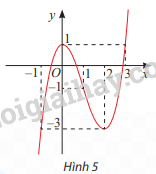
Quan sát đồ thị của hàm số $y = f\left( x \right) = {x^3}-3{x^2} + 1{\rm{ }}$ trong Hình 5.

a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi $x \ne 0$.

b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi $x \ne 2$.

c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi $x \ne 1$ hoặc f(x) < f(1) với mọi $x \ne 1$?

Quan sát đồ thị

a) Trên khoảng (-1; 2), f(x) < f(0) với mọi $x \ne 0$

b) Trên khoảng (0; 3), f(x) > f(2) với mọi $x \ne 2$

c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi $x \ne 1$ hoặc f(x) < f(1) với mọi $x \ne 1$

Thực hành4

Trả lời câu hỏi Thực hành 4 trang 11

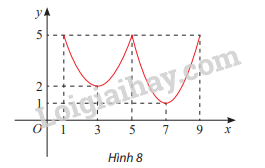
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8

Quan sát đồ thị

Hàm số y = f (x) có:

x = 5 là điểm cực đại vì f (x) < f(5) với mọi $x \in \left( {3;{\rm{ 7}}} \right)\backslash \left\{ 5 \right\}$, ${y_{cd}} = f(5) = 5$

x = 3 là điểm cực tiểu vì f(x) > f(3) với mọi $x \in \left( {1;{\rm{ 5}}} \right)\backslash \left\{ 3 \right\}$, ${y_{ct}} = f(3) = 2$

x=7 là điểm cực tiểu vì f(x) > f(7) với mọi $x \in \left( {5;{\rm{ 9}}} \right)\backslash \left\{ 7 \right\}$, ${y_{ct}} = f(7) = 1$

Khám phá3

Trả lời câu hỏi Khám phá 3 trang 11

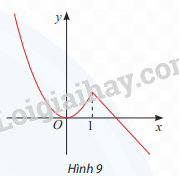
Đồ thị của hàm số $y = \left\{ \begin{array}{l}{x^2}{\rm{ }}khi{\rm{ }}x \le 1{\rm{ }}\\2 - x{\rm{ }}khi{\rm{ }}x > 1\end{array} \right.$ được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.

b) Tại x = 1, hàm số có đạo hàm không?

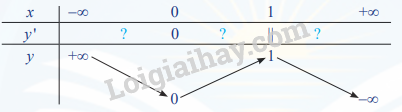
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y’ khi x đi qua điểm cực đại và điểm cực tiểu.

Quan sát đồ thị

a) Hàm số y = f (x) có:

x = 1 là điểm cực đại vì f (x) < f(1) với mọi $x \in \left( {0;{\rm{ + }}\infty } \right)\backslash \left\{ 0 \right\}$

x = 0 là điểm cực tiểu vì f(x) > f(0) với mọi $x \in \left( { + \infty ;{\rm{ 1}}} \right)\backslash \left\{ 0 \right\}$

b) Tại x = 1, hàm số không có đạo hàm vì đồ thị bị gấp khúc

c)

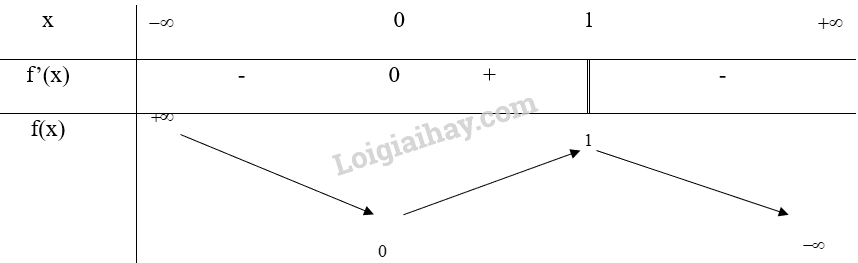
Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì y’ đổi dấu

Thực hành5

Trả lời câu hỏi Thực hành 5 trang 12

Tìm cực trị của hàm số $g\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}$

Tìm tập xác định, g’(x) và lập bảng biến thiên

Tập xác định: $D = \mathbb{R}\backslash \{ - 1\}$

$g'(x) = \frac{{{x^2} + 2x - 3}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.$

Bảng biến thiên:

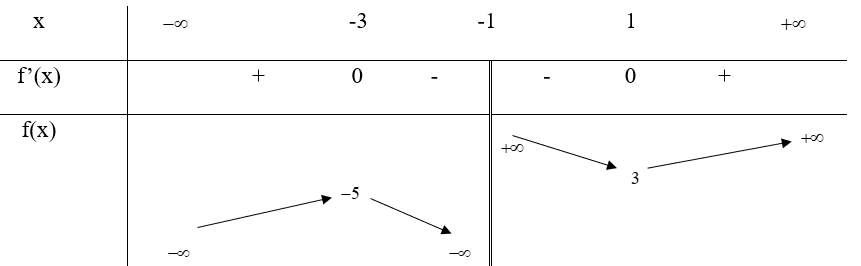
Vậy hàm số đạt cực tiểu tại x = -3, ${y_{ct}} = f( - 3) = - 5$, đạt cực đại tại x = 1, ${y_{cd}} = f(1) = 3$

Vận dụng2

Trả lời câu hỏi Vận dụng 2 trang 12

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840$ với $0 \le x \le 2000$

Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000]

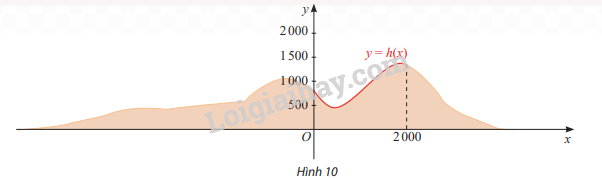
Tìm h’(x) và lập bảng biến thiên

Tập xác định: $D = [0;2000]$

$h'(x) = - \frac{1}{{440000}}{x^2} + \frac{9}{{1760}}x - \frac{{81}}{{44}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1800\\x = 450\end{array} \right.$

Bảng biến thiên:

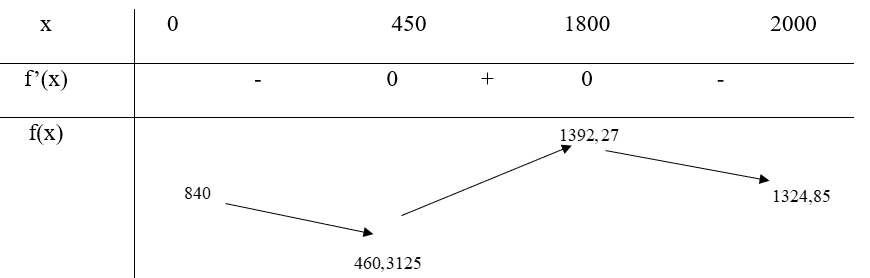
Vậy trên đoạn [0; 2000]:

Tọa độ đỉnh cực tiểu của dãy núi là (450; 460,3125)

Tọa độ đỉnh cực đại của dãy núi là (1800; 1392,27)