Giải mục 3 trang 22, 23, 24 Toán 12 tập 1 - Chân trời sáng tạo: Cho đồ thị của hàm số $y = \frac{{{x^2} + 1}}{x}$ và đường thẳng y = x...

Khám phá3

Trả lời câu hỏi Khám phá 3 trang 22

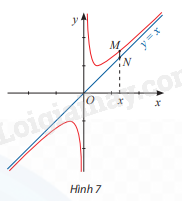
Cho đồ thị của hàm số $y = \frac{{{x^2} + 1}}{x}$ và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).

a) Tính $\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)$ và $\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)$

b) Tính MN theo x và nhận xét về MN khi $x \to + \infty$ hoặc $x \to - \infty$

Quan sát đồ thị

a) Tập xác định: $D = \mathbb{R}\backslash \left\{ 0 \right\}$

Ta có: $\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x} = 0$; $\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0$

Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x

b) MN = y – x = $\frac{{{x^2} + 1}}{x} - x = \frac{1}{x}$

Khi $x \to + \infty$ hoặc $x \to - \infty$ thì MN tiến dần về 0

Thực hành3

Trả lời câu hỏi Thực hành 3 trang 24

Tìm tiệm cận xiên của đồ thị hàm số $y = \frac{{2{x^2} - 3x}}{{x + 5}}$

Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0$ hoặc $\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0$

Tập xác định: $D = \mathbb{R}\backslash \left\{ { - 5} \right\}$

Ta có: $a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x}}{{x + 5}}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{{x^2} + 5x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{3}{x}}}{{1 + \frac{5}{x}}} = 2$

$b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^2} - 3x}}{{x + 5}} - 2x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13x}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13}}{{1 + \frac{5}{x}}} = - 13$

Ta có: $\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [y - (2x - 3)] = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{x + 5}} - (2x - 13) = \mathop {\lim }\limits_{x \to + \infty } \frac{{65}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{65}}{x}}}{{1 + \frac{5}{x}}} = 0$

Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x - 13

Thực hành4

Trả lời câu hỏi Thực hành 4 trang 24

Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: $C(x) = \frac{{50x + 2000}}{x}$

Tìm các đường tiệm cận của hàm số C(x).

- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: $\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty$

- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\mathop {\lim }\limits_{x \to - \infty } f(x) = m$ hoặc $\mathop {\lim }\limits_{x \to + \infty } f(x) = m$

- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0$ hoặc $\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0$

Tập xác định: $D = \mathbb{R}\backslash \left\{ 0 \right\}$

$\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty$; $\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty$

Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x = 0

$\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50$; $\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50$

Vậy tiệm cận ngang của đồ thị hàm số là đường thẳng y = 50