Khám phá4
Trả lời câu hỏi Khám phá 4 trang 46
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình 17).
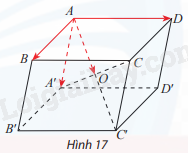
a) Tìm vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} \)
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a) và vectơ \(\overrightarrow {AO} \).

Áp dụng quy tắc hình hộp

a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \)
b) \(\overrightarrow {AC’} = 2\overrightarrow {AO} \)
Thực hành7
Trả lời câu hỏi Thực hành 7 trang 47
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ (Hình 19). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {CC’} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
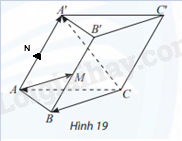

Áp dụng quy tắc hiệu, quy tắc hình bình hành và 2 vecto bằng nhau

Gọi N là trung điểm AA’
Ta có: \(\overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {CC’} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA’} = \overrightarrow {AB} + \overrightarrow {AN} = \overrightarrow {AM} \)
Advertisements (Quảng cáo)
Hay \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
Vận dụng3
Trả lời câu hỏi Vận dụng 3 trang 48
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) (Hình 21).
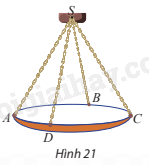
a) Sử dụng công thức \(\overrightarrow P = m\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn 10\(m/{s^2}\), tìm độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.

a) Áp dụng công thức tính trọng lực
b) Để chiếc đèn cân bằng thì hợp lực của 4 sợi xích phải cân bằng với trọng lực. Dựa vào tính chất của hình chóp tứ giác đều và quy tắc hình bình hành để tìm hợp lực đó rồi tìm ra lực căng của mỗi sợi xích

a) Độ lớn trọng lực tác động lên đèn chùm là: P = mg = 5.10 = 50N
b) Ta có S.ABCD là hình chóp tứ giác đều => SA = SB = SC = SD
Mà \(\widehat {ASC} = 60^\circ \) => Tam giác SAC đều
Gọi O là trung điểm AC.
Ta có: Hợp lực của 4 sợi xích là: \(\overrightarrow F = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \)
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay \(4\overrightarrow {SO} = \overrightarrow P \) hay 4SO = P \( \Leftrightarrow \)SO = 12,5
Xét tam giác đều SAC: \(SA = \frac{{\sqrt 3 }}{2}SO = \frac{{25\sqrt 3 }}{4}\)
Vậy độ lớn của lực căng cho mỗi sợi xích là \(\frac{{25\sqrt 3 }}{4}\)N
