. Bài 15 trang 17 SGK Đại số và Giải tích 12 Nâng cao - Bài 2. Cực trị của hàm số
Bài 15. Chứng minh rằng với mọi giá trị của \(m\), hàm số: \(y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}\) luôn có cực đại và cực tiểu

TXĐ: \(D = {\mathbb{R}}\backslash \left\{ m \right\}\)
\(\eqalign{
& y’ = {{\left[ {2x - m\left( {m + 1} \right)} \right]\left( {x - m} \right) - \left[ {{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \right]} \over {{{\left( {x - m} \right)}^2}}} \cr
& \,\,\,\,\, = {{{x^2} - 2mx + {m^2} - 1} \over {{{\left( {x - m} \right)}^2}}},x \ne m \cr} \)
Advertisements (Quảng cáo)
\(\eqalign{
& y’ = 0 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0 \Leftrightarrow {\left( {x - m} \right)^2} = 1 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \matrix{
x = m - 1;f\left( {m - 1} \right) = - {m^2} + m - 2 \hfill \cr
x = m + 1;f\left( {m + 1} \right) = - {m^2} + m + 2 \hfill \cr} \right. \cr} \)
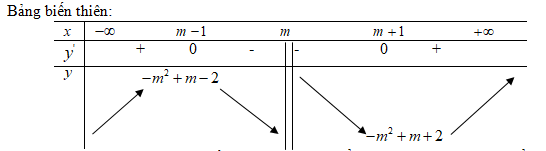
Với mọi giá trị của \(m\), hàm số đạt cực đại tại điểm \(x=m-1\) và đạt cực tiểu tại điểm \(x=m+1\)
Baitapsgk.com
