Bài 1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :
a) \(y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10\) ;
b) \(y{\rm{ }} = {\rm{ }}x{^4} + {\rm{ }}2{x^2}-{\rm{ }}3\) ;
c) \(y = x + {1 \over x}\)
d) \(y{\rm{ }} = {\rm{ }}{x^3}{\left( {1{\rm{ }}-{\rm{ }}x} \right)^{2}}\);
e) \(y = \sqrt {{x^2} - x + 1}\)

a) Tập xác định: \(D = \mathbb R\)
\(\eqalign{
& y’ = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y’ = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 2\left( {y = - 54} \right) \hfill \cr
x = - 3\left( {y = 71} \right) \hfill \cr} \right. \cr} \)
Bảng biến thiên:

Hàm số đạt cực trị tại \(x = -3\) và \(y\)CĐ \(= 71\)
Hàm số đạt cực tiểu tại \(x = 2\) và \(y\)CT \(= -54\)
b) Tập xác định: \(D =\mathbb R\)
\(y’ = 4{{\rm{x}}^3} + 4{\rm{x}} = 4{\rm{x}}\left( {{x^2} + 1} \right)\);
\(y’ = 0 \Leftrightarrow x = 0\left( {y = - 3} \right)\)
Bảng biến thiên:

Hàm số có điểm cực tiểu tại \(x = 0\) và \(y\)CT \(= -3\)
Advertisements (Quảng cáo)
c) Tập xác định: \(D = \mathbb R\)\ { 0 }
\(\eqalign{
& y’ = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};y’ = 0 \cr
& \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \matrix{
x = 1\left( {y = 2} \right) \hfill \cr
x = - 1\left( {y = - 2} \right) \hfill \cr} \right. \cr}\)
Bảng biến thiên

Hàm số đạt cực đại tại \(x = -1\), \(y\)CĐ \(= -2\)
Hàm số đạt cực tiểu tại \(x = 1\), \(y\)CT \(= 2\)
d) Tập xác định \(D = \mathbb R\)
\( y’ = 3{{\rm{x}}^2}{\left( {1 - x} \right)^2} - 2{{\rm{x}}^3}\left( {1 - x} \right) \)
\(= {x^2}\left( {1 - x} \right)\left( {3 - 5{\rm{x}}} \right)\)
\(\eqalign{
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 1\left( {y = 0} \right) \hfill \cr
x = {3 \over 5}\left( {y = {{108} \over {3125}}} \right) \hfill \cr
x = 0 \hfill \cr} \right. \cr} \)
Bảng biến thiên:
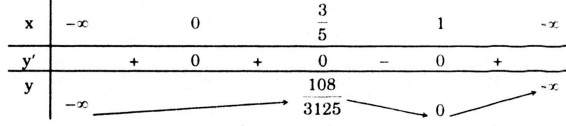
Hàm số đạt cực đại tại \(x = {3 \over 5};y = {{108} \over {3125}}\)
Hàm số đạt cực tiểu tại \(x = 1\), \(y\)CT =\( 0\)
e) Vì \(x^2\) –\( x + 1 > 0, ∀ ∈ \mathbb R\) nên tập xác định : \(D = \mathbb R\)
\(y’ = {{2{\rm{x}} - 1} \over {2\sqrt {{x^2} - x + 1} }};y = 0 \Leftrightarrow x = {1 \over 2}\left( {y = {{\sqrt 3 } \over 2}} \right)\)
Bảng biến thiên:

Hàm số đạt cực tiểu tại \(x = {1 \over 2};{y_{CT}} = {{\sqrt 3 } \over 2}\)
