Bài 2. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
a) \(y=- {x^4} + 8{x^{2}}-1\); b) \(y= {x^4} - 2{x^2} + 2\);
c) \(y = {1 \over 2}{x^4} + {x^2} - {3 \over 2}\); d) \(y = - 2{x^2} - {x^4} + 3\).

a) Tập xác định: \(\mathbb R\) ;
Sự biến thiên:
\(y’ =-4x^3+ 16x = -4x(x^2- 4)\);
\( y’ = 0 ⇔ x = 0, x = ±2\) .
- Hàm số đồng biến trên khoảng \((-\infty;-2)\) và \((0;2)\); nghịch biến trên khoảng \((-2;0)\) và \(2;+\infty)\).
- Cực trị:
Hàm số đạt cực đạt tại hai điểm \(x=-2\) và \(x=2\); \(y_{CĐ}=y(\pm 2)=15\).
Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=-1\)
- Giới hạn:
\(\mathop {\lim y}\limits_{x \to \pm \infty } = - \infty \)
Bảng biến thiên :
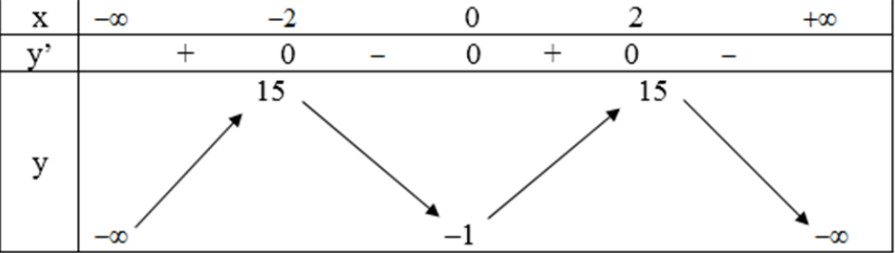
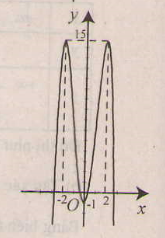
Đồ thị giao \(Oy\) tại điểm \((0;-1)\)
Hàm số đã cho là hàm số chẵn nhận trục \(Oy\) làm trục đối xứng.
Đồ thị
b) Tập xác định: \(\mathbb R\);
Sự biến thiên:
\(y’ =4x^3- 4x = 4x(x^2- 1)\);
\(y’ = 0 ⇔ x = 0, x = ±1\) .
- Hàm số đồng biến trên khoảng \((-1;0)\) và \((1;+\infty)\); nghịch biến trên khoảng \((-\infty;-1)\) và \((0;1)\).
- Cực trị:
Hàm số đạt cực đại tại \(x=0\); \(y_{CĐ}=2\).
Hàm số đạt cực tiểu tại hai điểm \(x=-1\) và \(x=1\); \(y_{CT}=y(\pm 1)=1\).
-Giới hạn:
\(\mathop {\lim y}\limits_{x \to \pm \infty } = + \infty \)
Bảng biến thiên :
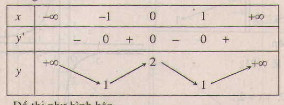
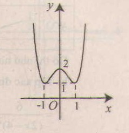
Hàm số đã cho là hàm số chẵn nhận trục \(Oy\) làm trục đối xứng.
Advertisements (Quảng cáo)
Đồ thị giao \(Oy\) tại điểm \((0;2)\)
Đồ thị
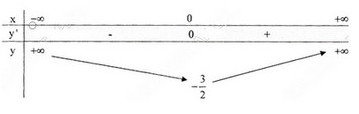
c) Tập xác định: \(\mathbb R\);
Sự biến thiên:
\(y’ =2x^3+ 2x = 2x(x^2+1)\);
\(y’ = 0 ⇔ x = 0\).
- Hàm số nghịch biến trên khoảng \((-\infty;0)\); đồng biến trên khoảng \((0;+\infty)\).
-Cực trị:
Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}={-3\over 2}\)
-Giới hạn:
\(\mathop {\lim y}\limits_{x \to \pm \infty } = + \infty \)
Bảng biến thiên :
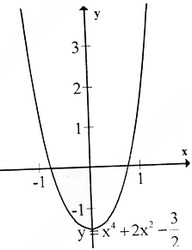
Hàm số đã cho là hàm số chẵn, nhận trục \(Oy\) làm trục đối xứng.
Đồ thị giao \(Ox\) tại hai điểm \((-1;0)\) và \((1;0)\); giao \(Oy\) tại \((0;{-3\over 2})\).
Đồ thị như hình bên.
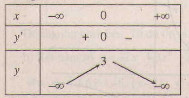
d) Tập xác định: \(\mathbb R\);
Sự biến thiên:
\(y’ = -4x - 4x^3= -4x(1 + x^2)\);
\(y’ = 0 ⇔ x = 0\).
- Hàm số đồng biến trên khoảng: \((-\infty;0)\); nghịch biến trên khoảng: \((0;+\infty)\).
- Cực trị: Hàm số đạt cực đạt tại \(x=0\); \(y_{CĐ}=3\).
- Giới hạn:
\(\mathop {\lim y}\limits_{x \to \pm \infty } = -\infty \)
Bảng biến thiên :
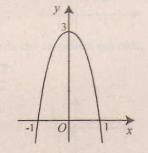
Hàm số đã cho là hàm chẵn, nhận trục \(Oy\) làm trục đối xứng.
Đồ thị giao \(Ox\) tại hai điểm \((1;0)\) và \((-1;0)\); giao \(Oy\) tại điểm \((0;3)\).
Đồ thị như hình bên.
 .
.
