Lý thuyết khảo sát sự biến thiên và vẽ đồ thị của hàm số: Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số...

Tóm tắt lý thuyết

1. Các bước khảo sát và vẽ đồ thị hàm số y = f(x)

a) Tìm tập xác định của hàm số. Xét tính chẵn, lẻ, tuần hoàn của hàm số để thu hẹp phạm vi khảo sát.

b) Sự biến thiên : 

+ Xét sự biến thiên của hàm số :

 - Tìm đạo hàm bậc nhất y’ ;

 - Tìm các điểm tại đó y’ bằng 0 hoặc không xác định ;

 - Xét dấu y’ và suy ra chiều biến thiên của hàm số .

+ Tìm cực trị .

+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).

+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị .

c) vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . .).

2. Bảng tóm tắt một số dạng đồ thị thường gặp

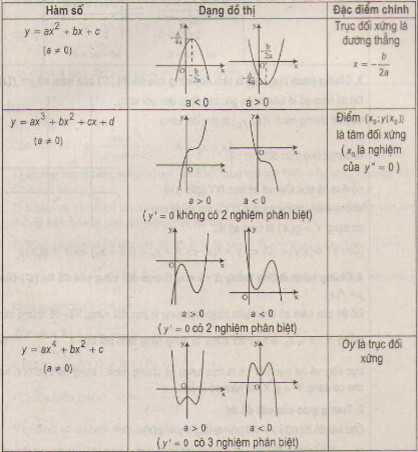
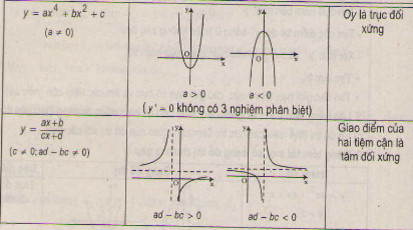
3.Chứng minh  $(x_{0};y_{0})$ là tâm đối xứng của đồ thị (C) của hàm số y=f(x)

Đồ thị hàm số lẻ luôn nhận gốc tọa độ là tâm đối xứng.

Vậy để chứng minh $I(x_{0};y_{0})$ là tâm đối xứng, ta dùng công thức đổi trục: $\left\{\begin{matrix} x=x_{0}+X & \\ y=y_{0}+Y & \end{matrix}\right.$ để đưa hệ trục Oxy về hệ trục IXY (gốc I) và chứng minh: trong hệ trục IXY, hàm số đã cho có dạng Y=g(X) là hàm số lẻ.

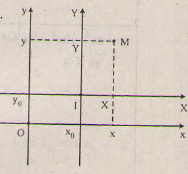
(Chú ý: $M(x,y)\in (C)\Leftrightarrow y=f(x)\Leftrightarrow Y+y_{0}=f(X+x_{0})\Leftrightarrow Y=g(X)$).

4. Chứng minh đường thẳng $\Delta : x=x_{0}$ là trục đối xứng của đồ thị (C) của hàm số y=f(x)

Đồ thị của hàm số chẵn luôn nhận trục tung là trục đối xứng. Vậy để chứng minh đường thẳng $\Delta : x=x_{0}$ là trục đối xứng, ta dùng công thức đổi trục $\left\{\begin{matrix} x=x_{0}+X & \\ y=Y & \end{matrix}\right.$ để đưa hệ số Oxy về hệ trục IXY ($\Delta$ là trục tung) và chứng minh: trong hệ trục IXY, hàm số đã cho có dạng Y=g(X) là hàm số chẵn.

5. Tương giao của các đồ thị

Cho hai đồ thị $(C_{1}):y=f(x);$ và $(C_{2}):y=g(x).$

Phương trình xác định hoành độ giao điểm của $(C_{1})$ và $(C_{2})$ là: f(x)=g(x). (1)

- Nếu (1) vô nghiệm thì $(C_{1})$ và $(C_{2})$ không có điểm chung (không cắt nhau và không tiếp xúc với nhau).

- Nếu (1) có nnghiệm phân biệt thì  $(C_{1})$ và $(C_{2})$ giao nhau tại n điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.

Chú ý

a)  $(C_{1})$ tiếp xúc với $(C_{2})$ $\Leftrightarrow$ hệ $\left\{ \begin{matrix} f(x) =g(x)& \\ f'(x)=g'(x) & \end{matrix}\right.$ có nghiệm. Nghiệm của hệ là hoành độ tiếp điểm của hai đồ thị đó.

b) Đường thẳng (d): y: mx+n tiếp xúc với parabol $-1$ $\Leftrightarrow$ hệ $\left\{ \begin{matrix} ax^{2}+bx+c=mx+n \\ 2ax+b=m) & \end{matrix}\right.$ có nghiệm 

$\Leftrightarrow$ phương trình $\Leftrightarrow$ $ax^{2}+bx+c=mx+n$ có nghiệm kép.