Bài 5. Tìm \(a\) và \(b\) để các cực trị của hàm số
\(y=\frac{5}{3}a^{2}x^{3}+2ax^{2}-9x+b\)
đều là những số dương và \(x_{0}=-\frac{5}{9}\) là điểm cực đại.

- Xét \(a = 0\) hàm số trở thành \(y = -9x + b\). Trường hợp này hàm số không có cực trị.
- Xét \(a \ne 0\). Ta có : \(y{\rm{ }} = {\rm{ }}5{a^2}{x^2} + {\rm{ }}4ax{\rm{ }}-{\rm{ }}9\); \(y’= 0 \)\(⇔ x=-\frac{1}{a}\) hoặc \(x=-\frac{9}{5a}\)
- Với \(a < 0\) ta có bảng biến thiên :
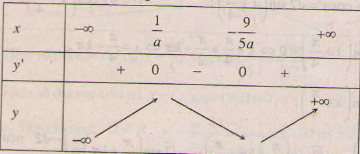
Theo giả thiết \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(\frac{1}{a}=-\frac{5}{9}\Leftrightarrow a=\frac{9}{5}\). Theo yêu cầu bài toán thì
Advertisements (Quảng cáo)
\(y_{(CT)}=y\left ( -\frac{9}{5a} \right )=y(1)>0\)
\(\Leftrightarrow \frac{5}{3}\cdot \left ( -\frac{9}{5} \right )^{2}+2\cdot \left ( -\frac{9}{5} \right )-9+b>0\Leftrightarrow b>\frac{36}{5}.\)
- Với \(a > 0\) ta có bảng biến thiên :
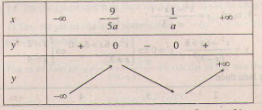
Vì \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(-\frac{9}{5a}=-\frac{5}{9}\Leftrightarrow a=\frac{81}{25}\). Theo yêu cầu bài toán thì: \(y_{(ct)}=y\left ( \frac{1}{a} \right )=y\left ( \frac{25}{81} \right )>0\)
\(\Leftrightarrow \frac{5}{3}\cdot \left ( \frac{81}{25} \right )^{2}\left ( \frac{25}{81} \right )^{3}+2.\frac{81}{25}\cdot \left ( \frac{25}{81} \right )^{2}-9\cdot \frac{25}{81}+b>0\)
\(\Leftrightarrow b>\frac{400}{243}.\)
Vậy các giá trị \(a, b\) cần tìm là:
\(\left\{\begin{matrix} a=-\frac{9}{5} & \\ b>\frac{36}{5} & \end{matrix}\right.\) hoặc \(\left\{\begin{matrix} a=\frac{81}{25} & \\ b>\frac{400}{243} & \end{matrix}\right.\).
