Bài 6. Xác định giá trị của tham số \(m\) để hàm số \(y=\frac{x^{2}+mx+1}{x+m}\) đạt cực đại tại \(x = 2\).

Tập xác định : \(D=\mathbb{R}\setminus \left \{ -m \right \};\)
\(y’=\frac{2x^{2}+2mx+m^{2}-1}{(x+m)^{2}}.\)
Nếu hàm số đạt cực đại tại \(x = 2\) thì \(y'(2) = 0\) \(⇔ {m^{2}} + {\rm{ }}4m{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\)\( ⇔ m=-1\) hoặc \(m=-3\)
- Với \(m = -1\), ta có : \(y=\frac{x^{2}-x+1}{x-1};\)
\(y’=\frac{x^{2}-2x}{(x-1)^{2}}; y’=0\Leftrightarrow \left\{\begin{matrix} x^{2} -2x=0& \\ x\neq 1 & \end{matrix}\right.\)
\(\Leftrightarrow x=0\) hoặc \(x=2\).
Ta có bảng biến thiên :
Advertisements (Quảng cáo)
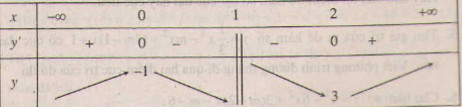
Trường hợp này ta thấy hàm số không đạt cực đại tại \(x = 2\).
- Với \(m = -3\), ta có: \(y=\frac{x^{2}3x+1}{x-3};\)
\(y’=\frac{x^{2}-6x+8}{(x-3)^{2}};y’=0\Leftrightarrow \left\{\begin{matrix} x^{2-6x+8=0} & \\ x\neq 3 & \end{matrix}\right.\)
\(\Leftrightarrow x=2\) hoặc \(x=4\)
Ta có bảng biến thiên :
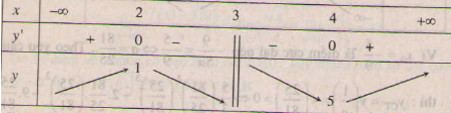
Trường hợp này ta thấy hàm số đạt cực đại tại \(x = 2\).
Vậy \(m = -3\) là giá trị cần tìm.
