Bài 5. Từ một điểm \(M\) nằm nằm bên ngoài mặt cầu \(S( O; r)\) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại \(A, B\) và \(C, D\).
a) Chứng minh rằng \(MA.MB = MC.MD\).
b) Gọi \(MO = d\). Tính \(MA.MB\) theo \(r\) và \(d\).
 :
:
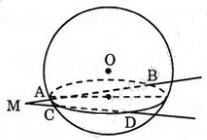
a) Gọi \((P)\) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng\((P)\) cắt mặt cầu \(S(O;r)\) theo một đường tròn tâm \(I\), là hình chiếu vuông góc của \(O\) lên mặt phẳng \((P)\).
Xét hai tam giác \(MAD\) và \(MCB\) có:
+) \(\widehat B = \widehat D\) (Hai góc cùng chắn một cung)
+) \(\widehat M\)
\( \Rightarrow \Delta MAD\) đồng dạng \(\Delta MCB\).
Advertisements (Quảng cáo)
\(\Rightarrow{{MA} \over {MC}} = {{MD} \over {MB}}\Rightarrow MA.MB=MC.MD\)
b) Đặt \(MO = d\), ta có \(OI\) vuông góc với \((P)\) và ta có:
\(O{M^2} = M{I^2} = O{I^2};O{A^2} = O{I^2} + I{A^2}\)
Hạ \(IH\) vuông góc \(AB\), ta có \(H\) là trung điểm của \(AB\).
Ta có \(MA = MH - HA\); \(MB = MH + HB = MH + HA\).
\(MA.MB = M{H^2} - H{A^2}\)
\(\eqalign{
& = (M{H^2} + H{I^2}) - (H{A^2} + I{H^2}) \cr
& = M{I^2} - I{A^2} \cr
& = (M{I^2} + O{I^2}) - (I{A^2} + O{I^2}) \cr
& = O{M^2} - O{A^2} \cr
& = {d^2} - {r^2} \cr} \)
Vậy \(MA.MB = {d^2} - {r^2}\).
