Bài 8. Cho hàm số \(y = {x^3} + (m + 3){x^2} + 1 - m\) (m là tham số) có đồ thị là (Cm).
a) Xác định \(m\) để hàm số có điểm cực đại là \(x=-1\).
b) Xác định \(m\) để đồ thị (Cm) cắt trục hoành tại \(x=-2\).
Hướng dẫn giải:
a) \(y’ = 3{x^2} + 2(m + 3)x = x\left[ {3x + 2(m + 3)} \right]\);
\(y’ = 0 \Leftrightarrow {x_1} = 0\) hoặc \({x_2} = - {{2m + 6} \over 3}\)
Xảy ra hai trường hợp đối với dấu của \(y’\):
Trường hợp 1: \(x_1<x_2\)
Bảng biến thiên:
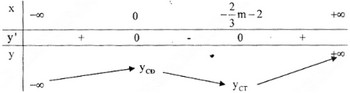
Advertisements (Quảng cáo)
Trường hợp này hàm số đạt cực đại tại \(x=0\) do đó trường hợp này loại.
Trường hợp 2: \(x_2<x_1\)
Bảng biến thiên:
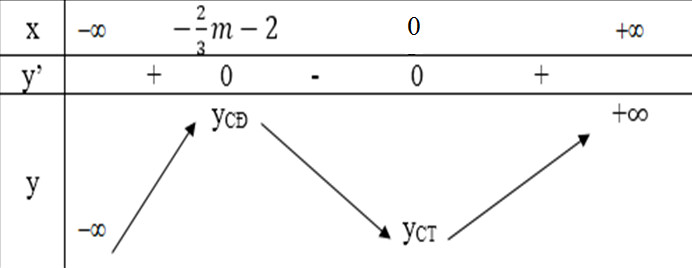
Để hàm số có điểm cực đại tại \(x = -1\) ta phải có
\({x_2} = - {{2m + 6} \over 3} = - 1 \Leftrightarrow m = - {3 \over 2}\)
(Chú ý : trường hợp \(x_1= x_2\) thì hàm số không có cực trị).
b) (Cm) cắt \(Ox\) tại \(x = -2\)\( ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔\) \(m = - {5 \over 3}\).
