So sánh các độ dài DN và EM. Câu 51 trang 144 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 5: Trường hợp bằng nhau của tam giác góc - cạnh - góc (g.c.g)
Cho tam giác ADE có \(\widehat D = \widehat E\). Tia phân giác của góc D cắt AE ở điểm M. Tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dài DN và EM.
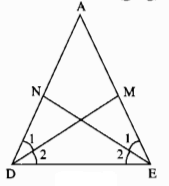
Tam giác ADE có: \(\widehat D = \widehat E\) (gt)
\(\widehat {{D_1}} = \widehat {{D_2}} = {1 \over 2}\widehat D\) (Vì DM là tia phân giác)
\(\widehat {{E_1}} = \widehat {{E_2}} = {1 \over 2}\widehat E\) (Vì EN là tia phân giác)
Suy ra: \(\widehat {{D_1}} = \widehat {{D_2}} = \widehat {{E_1}} = \widehat {{E_2}}\)
Advertisements (Quảng cáo)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat {N{\rm{D}}E} = \widehat {ME{\rm{D}}}\left( {gt} \right)\)
DE cạnh chung
\(\widehat {{D_2}} = \widehat {{E_2}}\) (chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).
.