Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở O. Kẻ \({\rm{OD}} \bot AC\), kẻ \({\rm{O}}E \bot AB\). Chứng minh rằng OD = OE.

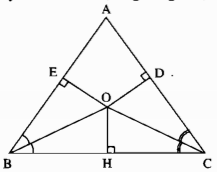
Kẻ \(OH \bot BC\)
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat {OEB} = \widehat {OHB} = 90^\circ \)
Cạnh huyền OB chung
\(\widehat {EBO} = \widehat {HBO}\) (gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
Advertisements (Quảng cáo)
\( \Rightarrow \) OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat {OHC} = \widehat {O{\rm{D}}C} = 90^\circ \)
Cạnh huyền OC chung
\(\widehat {HCO} = \widehat {DCO}\left( {gt} \right)\)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
\( \Rightarrow \) OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.
