Chứng minh rằng AB = HK, AH = BK.. Câu 52 trang 144 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 5: Trường hợp bằng nhau của tam giác góc - cạnh - góc (g.c.g)
Cho hình bên, trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK, AH = BK.
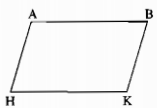

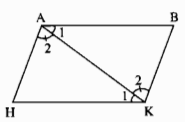
Nối AK. Ta có:
AB // HK (gt)
\( \Rightarrow \widehat {{A_1}} = \widehat {{K_1}}\) (hai góc so le trong)
AH // BK (gt)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {{A_2}} = \widehat {{K_2}}\) (hai góc so le trong)
Xét ∆ABK và ∆KHA, ta có:
\(\widehat {{A_1}} = \widehat {{K_1}}\) (chứng minh trên)
AK cạnh chung
\(\widehat {{A_2}} = \widehat {{K_2}}\) (chứng minh trên)
Suy ra: ∆ABK = ∆KHA (g.c.g)
Vậy AB = KH, BK = AH (2 cạnh tương ứng)
