Tính chu vi tam giác ACD. Câu 59 trang 145 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 5: Trường hợp bằng nhau của tam giác góc - cạnh - góc (g.c.g)
Cho tam giác ABC có AB = 2,5cm, AC = 3cm, BC = 3,5cm. Qua A vẽ đường thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau ở D. Tính chu vi tam giác ACD.
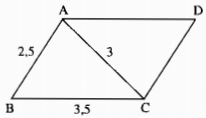
Ta có: AB // CD (gt)
Suy ra: \(\widehat {AC{\rm{D}}} = \widehat {CAB}\) (2 góc so le trong)
BC // AD (gt)
Suy ra: \(\widehat {{\rm{CAD}}} = \widehat {ACB}\) (2 góc so le trong)
Advertisements (Quảng cáo)
Xét ∆ABC = ∆CDA, ta có:
\(\widehat {AC{\rm{D}}} = \widehat {CAB}\) (chứng minh trên)
AC cạnh chung
\(\widehat {CA{\rm{D}}} = \widehat {ACB}\) (chứng minh trên)
Suy ra: ∆ABC = ∆CDA (g.c.g)
Suy ra: CD = AB = 2,5(cm) và AD = BC = 3,5 (cm)
Chu vi ∆ACD là: AC + AD + CD = 3 + 3,5 + 2,5 = 9 (cm)