Advertisements (Quảng cáo)
Cho hình dưới trong đó DE // AB, DF // AC, EF // BC. Tính chu vi tam giác DFE.
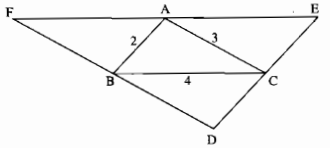
Xét ∆ABC và ∆ ABF, ta có:
\(\widehat {ABC} = \widehat {{\rm{BAF}}}\) (so le trong)
AB cạnh chung
\(\widehat {BAC} = \widehat {ABF}\) (so le trong)
Suy ra: ∆ABC = ∆ ABF (g.c.g)
Suy ra: AF = BC = 4 (2 cạnh tương ứng)
BF = AC = 3 (2 cạnh tương ứng)
Xét ∆ABC và ∆ACE, ta có:
\(\widehat {ACB} = \widehat {CA{\rm{E}}}\) (so le trong)
AC cạnh chung
\(\widehat {BAC} = \widehat {EC{\rm{A}}}\) (so le trong)
Suy ra: ∆ABC = ∆CEA (g.c.g)
Suy ra: AE = BC = 4 (2 cạnh tương ứng)
Advertisements (Quảng cáo)
CE = AB = 2 (2 cạnh tương ứng)
Xét ∆ABC và ∆DCB, ta có:
\(\widehat {ACB} = \widehat {DBC}\) (so le trong)
BC cạnh chung
\(\widehat {ABC} = \widehat {DCB}\) (so le trong)
Suy ra: ∆ABC = ∆DCB (g.c.g)
Suy ra: DC = AB = 2 (2 cạnh tương ứng)
DB = AC = 3 (2 cạnh tương ứng)
Ta có: EF = AE + AF = 4 + 4 = 8
DF = DB + BF = 3 + 3 = 6
DE = DC + CE = 2 + 2 = 4
Vậy chu vi ∆DEF là:
DE + DF + EF = 4 + 6 + 8 = 18 (đơn vị độ dài)
Mục lục môn Toán 7 (SBT)