
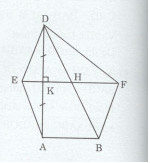
Cho tam giác DEF nhọn, kẻ \(DK \bot EF(K \in EF)\) . Trên tia đối của tia KD, lấy điểm A sao cho KA = KD.
a) Chứng minh rằng \(\Delta DKE = \Delta AKE\)
b) Chứng minh rằng EF là tia phân giác của góc DEA.
c) Chứng minh rằng \(\widehat {EDF} = \widehat {EAF}\)
d) Gọi H là trung điểm EF, trên tia đối của tia HD ta lấy điểm B sao cho H là trung điểm của DB. Chứng minh rằng BF = AE.

a)Xét tam giác DKE và AKE có:
DK = AK (giả thiết)
\(\widehat {DKE} = \widehat {AKE}( = {90^0})\)
KE là cạnh chung.
Do đó: \(\Delta DKE = \Delta AKE(c.g.c)\)
b) Ta có: \(\Delta DKE = \Delta AKE\) (chứng minh câu a) \( \Rightarrow \widehat {DEK} = \widehat {AEK}.\)
Advertisements (Quảng cáo)
Vậy EF là tia phân giác của góc DEA.
c) Xét tam giác DEF và AEF có:
\(DE = AE(\Delta DKE = \Delta AKE)\)
\(\widehat {DEF} = \widehat {AEF}\) (chứng minh câu b)
EF là cạnh chung.
Do đó: \(\Delta DEF = \Delta AEF(c.g.c) \Rightarrow \widehat {EDF} = \widehat {EAF}\)
d) Xét tam giác HED và HFB có:
HD = HB (H là trung điểm của BD)
\(\widehat {DHE} = \widehat {FHB}\) (hai góc đối đỉnh)
HE = HF (H là trung điểm của EF)
Do đó: \(\Delta HED = \Delta HFB(c.g.c) \Rightarrow DE = BF\)
Mà DE = AE \((\Delta DKE = \Delta AKE)\) nên AE = BF.
