
Cho hình 17.
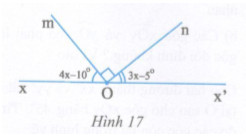
a) Tính số đo \(\widehat {xOm}\) và \(\widehat {x’On}\)
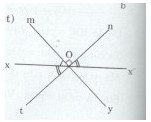
b) Vẽ tia Ot sao cho \(\widehat {xOt}\) và \(\widehat {nOx’}\) là hai góc đối đỉnh. Trên nửa mặt phẳng bờ xx’ chứa tia Ot, vẽ tia Oy sao cho \(\widehat {tOy} = {90^o}\). Hai góc mOn và tOy có là hai góc đối đỉnh không ? Vì sao ?

a)Ta có: \(\widehat {xOm} + \widehat {mOn} + \widehat {n0x’} = {180^0}\) (vì góc xOx’ là góc bẹt)
Nên \(4x - {10^0} + {90^0} + 3x - {5^0} = {180^0}.\)
Do đó: \(\eqalign{ & 7x = {180^0} - {90^0} + {10^0} + {5^0} = {105^0}. \cr & \Rightarrow x = {105^0}:7 = {15^0} \cr} \)
Advertisements (Quảng cáo)
Vậy \(\widehat {xOm} = 4x - {10^0} = 4.15 - {10^0} = {50^0}.\)
Và \(\widehat {x’On} = 3x - {5^0} = 3.15 - {5^0} = {40^0}.\)
b) Ta có: góc xOt và nOx’ là hai góc đối đỉnh
=> On và Ot là hai tia đối nhau \( \Rightarrow \widehat {nOt} = {180^0}.\)
Do đó:
\(\eqalign{ & \widehat {n0x’} + \widehat {y0x’} + \widehat {yOt} = {180^0} \cr & \Rightarrow {40^0} + \widehat {y0x’} + {90^0} = {180^0} \Rightarrow \widehat {y0x’} = {180^0} - {90^0} - {40^0} = {50^0} \cr} \)
Ta có: \(\widehat {mOn} + \widehat {n0x’} + \widehat {y0x’} = {90^0} + {40^0} + {50^0} = {180^0}\)
\( \Rightarrow \widehat {mOy} = {180^0} \Rightarrow \) Om và Oy là hai tia đối nhau.
Vậy góc mOn và yOt là hai góc đối đỉnh.
