Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác - Bài tập 40 trang 125 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Tia AH cắt A, đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại I. Chứng minh I là trung điểm của BC.

Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Tia AH cắt A, đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại I. Chứng minh I là trung điểm của BC.

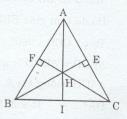
∆ABC có hai đường cao BE và CF cắt nhau tại H (gt)
=> H là trực tâm của ∆ABC.
Advertisements (Quảng cáo)
Mà AI đi qua H (gt). Nên AI là đường cao của ∆ABC.
∆ABC cân tại A có AI là đường cao.
Do đó AI là đường trung tuyến.
Vậy I là trung điểm của BC.
