Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác - Bài tập 4 trang 120 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC có AB = AC, BM và CN là hai trung tuyến.
Cho tam giác ABC có AB = AC, BM và CN là hai trung tuyến.
a) Chứng minh BM = CN.
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.
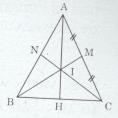
a) Ta có: \(AM = MC = {{AC} \over 2}\) (M là trung điểm của AC)
\(AN = NB = {{AB} \over 2}\) (N là trung điểm của AB)
AC = AB (gt)
Do đó: AM = MC = AN = NB.
Advertisements (Quảng cáo)
Xét ∆ABM và ∆ACN ta có: AB = AC (gt)
\(\widehat {BAM}\) (chung)
AM = AN
Do đó ∆ABM = ∆CAN (c.g.c) => BM = CN.
b) ∆ABC có: BM và CN là hai đường trung tuyến (gt)
I là giao điểm của BM và CN (gt)
=> I là trọng tâm của ∆ABC
Mà AH đi qua I (\(H \in BC\)). Vậy AH là đường trung tuyến của tam giác ABC.
Do đó H là trung điểm của BC.