Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác - Bài tập 7 trang 96 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC cân tại A có
Cho tam giác ABC cân tại A có \(\widehat {BAC} = {40^o}\) . So sánh độ dài các cạnh của tam giác ABC.
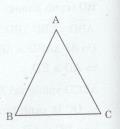
∆ABC cân tại A (gt) \( \Rightarrow \widehat B = \widehat C\)
∆ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ\)
Advertisements (Quảng cáo)
Do đó
\(\eqalign{ & 40^\circ + \widehat B + \widehat B = 180^\circ \Rightarrow 40^\circ + 2\widehat B = 180^\circ \cr & \Rightarrow 2\widehat B = 180^\circ - 40^\circ = 140^\circ \Rightarrow \widehat B = 70^\circ \cr}\)
∆ABC có \(\widehat A < \widehat B\) (vì 40⁰ < 70⁰)
=> BC < AC (định lí cạnh đối diện với góc lớn hơn)
Mà AB = AC (∆ABC cân tại A). Vậy BC < AC = AB.