Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác - Bài tập 6 trang 96 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC vuông tại B có M là trung điểm của BC
Cho tam giác ABC vuông tại B có M là trung điểm của BC. So sánh \(\widehat {BAM}\,\,\,\& \,\,\,\widehat {MAC}\)
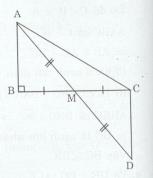
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
Xét ∆MCD và ∆MBA có: MD = MA
\(\widehat {CMD} = \widehat {BMA}\) (đối đỉnh)
MC = MB (M là trung điểm của BC)
Do đó ∆MCD = ∆MBA (c.g.c)
Advertisements (Quảng cáo)
\( \Rightarrow CD = AB,\widehat {CDM} = \widehat {BAM}\)
Mặt khác ∆ABC vuông tại B.
\( \Rightarrow \widehat {ABC}\) là góc lớn nhất trong ba góc
=> AC là cạnh lớn nhất trong ba cạnh (định lí cạnh đối diện với góc lớn hơn)
=> AC > AB. Nên AC > CD
∆ACD có AC > CD \( \Rightarrow \widehat {CDM} > \widehat {MAC}\) (định lí góc đối diện với cạnh lớn hơn)
Vậy \(\widehat {BAM} > \widehat {MAC}.\)