
Cho hình chữ nhật \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Lấy điểm \(M\) thuộc đoạn thẳng \(OC\). Gọi \(E,F\) lần lượt là hình chiếu của điểm \(M\) trên đường thẳng \(AB,AD\). Chứng minh:
a) Tứ giác \(AEMF\) là hình chữ nhật.
b) \(BD//EF\).

Dựa vào tính chất của hình chữ nhật:
- Hai cạnh đối song song và bằng nhau
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Advertisements (Quảng cáo)

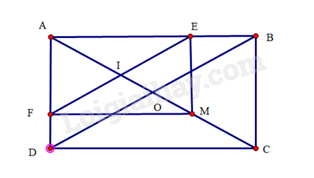
Gọi \(I\) là giao điểm của \(AM\) và \(EF\)
a) Tứ giác \(AEMF\) có \(\widehat {FAE} = \widehat {AEM} = \widehat {MFA} = 90^\circ \) nên \(AEMF\) là hình chữ nhật.
b) Do \(ABCD\) và \(AEMF\) là hình chữ nhật nên \(OA = OB\) và \(IA = IE\). Suy ra tam giác \(OAB\) cân tại \(O\) và tam giác \(IAE\) cân tại \(I\).
Do đó \(\widehat {OBA} = \widehat {OAB}\) và \(\widehat {IEA} = \widehat {IAE}\) hay \(\widehat {OBA} = \widehat {IEA}\).
Mà \(\widehat {OBA}\) và \(\widehat {IEA}\) nằm ở vị trí đòng vị, suy ra \(BD//EF\).
