
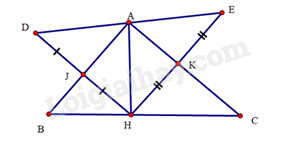
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\). Kẻ \(HJ\) vuông góc với \(AB\) tại \(J\) và \(HK\) vuông góc với \(AC\) tại \(K\). Trên tia \(HJ\) lấy điểm \(D\) sao cho \(DJ = JH\). Trên tia \(HK\) lấy điểm \(E\) sao cho \(EK = KH\).
a) Chứng minh \(A\) là trung điểm của \(DE\).
b) Tứ giác \(AJHK\) là hình gì? Vì sao?
c) Chứng minh \(BC = BD + CE\).

Dựa vào các dấu hiệu nhận biết của hình vuông, hình chữ nhật, hình bình hành để chứng minh.

a) Xét \(\Delta ADJ\) vuông tại \(J\) và \(\Delta AHJ\) vuông tại \(J\) có:
\(DJ = HJ\) (gt), \(AJ\) là cạnh chung
Do đó \(\Delta ADJ = \Delta AHJ\) (hai cạnh góc vuông)
Suy ra \(AD = AH\) (hai cạnh tương ứng) và \(\widehat {JAD} = \widehat {JAH}\) (hai góc tương ứng)
Tương tự ta cũng chứng minh được \(\Delta AHK = \Delta AEk\) (hai cạnh góc vuông)
Suy ra \(AH = AE\) (hai cạnh tương ứng) và \(\widehat {KAH} = \widehat {KAE}\) (hai góc tương ứng)
Ta có:
Advertisements (Quảng cáo)
\(\widehat {JAD} + \widehat {JAH} + \widehat {KAH} + \widehat {KAE} = 2\left( {\widehat {JAH} + \widehat {KAH}} \right) = 2.\widehat {JAK} = 2.90^\circ = 180^\circ \)
Hay \(\widehat {DAE} = 180^\circ \) nên ba điểm \(D,A,E\) thẳng hàng
Lại có \(AD = AH\) và \(AH = AE\) nên \(AD = AE\)
Do đó \(A\) là trung điểm của \(DE\).
b) Ta có \(AB \bot HE\) tại \(K\) nên \(\widehat {AJH} = 90^\circ \)
\(AC \bot HE\) tại \(K\) nên \(\widehat {AKH} = 90^\circ \)
Xét tứ giác \(AJKH\) có:
\(\widehat {AJH} = \widehat {JAK} = \widehat {AKH} = 90^\circ \) nên là hình chữ nhật.
c) Xét tam giác \(BDJ\) vuông tại \(J\) và tam giác \(BHJ\) vuông tại \(J\) có:
\(DJ = HJ\) (gt), \(BJ\) là cạnh chung
Do đó \(\Delta BDJ = \Delta BHJ\) (hai cạnh góc vuông)
Suy ra \(BD = BH\) (hai cạnh tương ứng)
Tương tự, ta cũng có \(\Delta CHK = \Delta CEK\) (hai cạnh góc vuông)
Suy ra \(CH = CE\) (hai cạnh tương ứng)
Khi đó \(BC = BH + CH = BD + CE\)
Vậy \(BC = BD + CE\).
