
Cho tứ giác \(ABCD\) có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\). Điều kiện của tứ giác \(ABCD\) để tứ giác \(EFGH\) là hình chữ nhật là:
A. \(BD = AC\)
B. \(AB \bot BC\)
C. \(BD \bot AC\)
D. \(AB = CD\)

Dựa vào dấu hiệu nhận biết các hình:
Hình chữ nhật, hình thoi, hình vuông để tìm ra điều kiện của hai đường chéo \(AC\) và \(BD\) tương ứng.

Advertisements (Quảng cáo)
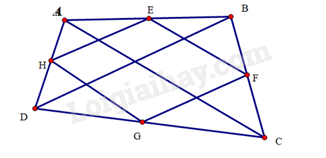
Nối \(AC,BD\)
Xét tam giác \(ABCD\) có \(E,H\) lần lượt là trung điểm của \(AB,AD\) nên \(EH\) là đường trung bình của tam giác \(ABD\).
Suy ra \(EH//BD,EH = \frac{1}{2}BD\) (1)
Tương tự xét tam giác \(CBD\) có \(F,G\) lần lượt là trung điểm của \(BC,CD\) nên \(Fg\) là đường trung bình của tam giác \(CBD\) suy ra \(FG//BD,FG = \frac{1}{2}BD\) (2)
Từ (1), (2) suy ra \(EH//FG;EH = FG\) nên \(EFGH\) là hình bình hành (dấu hiệu nhận biết).
Để hình bình hành \(EFGH\) là hình chữ nhật thì \(\widehat {EHG} = 90^\circ \) hay \(EH \bot HG\)
Lại có \(HG//AC\) (do \(HG\) là đường trung bình của tam giác \(DAC\)) nên \(EH \bot AC\) mà \(EH \bot BD\) (cmt) nên \(AC \bot BD\).
Vậy tứ giác \(ABCD\) cần có \(AC \bot BD\) thì \(EFGH\) là hình chữ nhật.
→ Đáp án đúng là đáp án C.
