
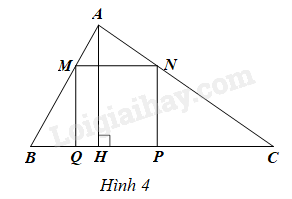
Cho tam giác \(ABC\) có cạnh \(BC = 2x\left( {dm} \right)\), đường cao \(AH = x\left( {dm} \right)\) với \(x > 0\) và hình vuông \(MNPQ\) có cạnh \(MN = y\left( {dm} \right)\) với \(y > 0\) (Hình 4).
a) Viết công thức tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\) dưới dạng tích.
b) Tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\), biết \(x - y = 2\) và \(x + y = 10\)

Advertisements (Quảng cáo)
Sử dụng công thức tính diện tích tam giác, công thức tính diện tích hình vuông và các phương pháp phân tích đa thức thành nhân tử để tính tổng diện tích các tam giác \(AMN,BMQ,CNP\).

a) Ta có:
\(\begin{array}{l}{S_{AMN + BMQ + NCP}} = {S_{ABC}} - {S_{MNPQ}}\\ = \frac{1}{2}\left( {x.2x} \right) - {y^2} = {x^2} - {y^2}\\ = \left( {x - y} \right)\left( {x + y} \right)\left( {d{m^2}} \right)\end{array}\)
b) Ta có:
\({S_{AMN + BMQ + NCP}} = 2.10 = 20\left( {d{m^2}} \right)\)
