
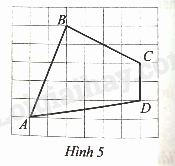
Tính chu vi của tứ giác \(ABCD\) ở Hình 5 (làm tròn kết quả đến hàng phần trăm của centimet). Biết rằng độ dài cạnh mỗi ô vuông là 1 cm.

Vẽ thêm các điểm \(M,N,P\) và áp dụng định lí Pythagore trong tam giác vuông: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Ta vẽ thêm các điểm \(M,N,P\) như hình vẽ:
Advertisements (Quảng cáo)
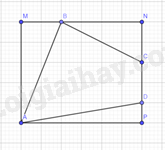
Ta có: \(AM = 5cm\), \(BM = 2cm\), \(BN = 4cm\), \(CN = 2cm\), \(CD = 2cm\), \(DP = 1cm\), \(AP = 6cm\)
\(A{B^2} = A{M^2} + B{M^2} = 29\) suy ra \(AB = \sqrt {29} cm\)
\(B{C^2} = B{N^2} + C{N^2} = 20\) suy ra \(BC = \sqrt {20} cm\)
\(D{A^2} = D{P^2} + A{P^2} = 37\) suy ra \(DA = \sqrt {37} cm\).
Chu vi của tứ giác \(ABCD\) là: \(\sqrt {29} + \sqrt {20} + 2 + \sqrt {37} \approx 17,94\left( {cm} \right)\).
