Chứng minh rằng MN = PQ.. Câu 10 trang 84 Sách bài tập (SBT) Toán 8 tập 2 - Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q (h.9)
Chứng minh rằng MN = PQ.
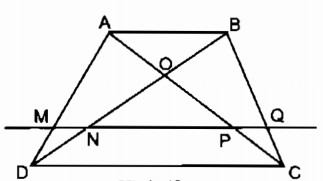
Trong tam giác ADB, ta có: MN // AB (gt)
Suy ra: \({{DN} \over {DB}} = {{MN} \over {AB}}\) (Hệ quả định lí Ta-lét ) (1)
Trong tam giác ACB, ta có: PQ // AB (gt)
Advertisements (Quảng cáo)
Suy ra: \({{CQ} \over {CB}} = {{PQ} \over {AB}}\) (Hệ quả định lí Ta-lét ) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong tam giác BDC, ta có: NQ // CD (chứng minh trên)
Suy ra: \({{DN} \over {DB}} = {{CQ} \over {CB}}\) (Định lí Ta-lét ) (3)
Từ (1), (2) và (3) suy ra: \({{MN} \over {AB}} = {{PQ} \over {AB}}\) hay MN = PQ.