Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng:
a. \({{OM} \over {ON}} = {{AB} \over {CD}}\)
b. \({{OH} \over {OK}} = {{BC} \over {AD}}\)

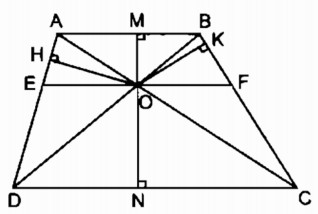
a. Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
\({{OM} \over {ON}} = {{MA} \over {NC}}\) hay \({{OM} \over {ON}} = {{MB} \over {ND}}\)
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:
\({{OM} \over {ON}} = {{MA} \over {NC}} = {{MB} \over {ND}} = {{MA + MB} \over {NC + ND}} = {{AB} \over {CD}}\)
Advertisements (Quảng cáo)
b. Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
\({S_{AEO}} = {S_{BFO}}\) (1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
\({S_{DEO}} = {S_{CFO}}\) (2)
Từ (1) và (2) suy ra :
\({S_{OAD}} = {S_{OBC}}\) (3)
Suy ra: \(OH.AD = OK.BC \Leftrightarrow {{OH} \over {OK}} = {{BC} \over {AD}}\)
