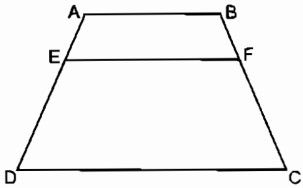
Cho hình thang ABCD (AB // CD). Trên cạnh bên AD lấy điểm E sao cho \({{AE} \over {ED}} = {p \over q}\) . Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F
Chứng minh rằng: \(EF = {{p.CD + q.AB} \over {p + q}}\)
HD: Kẻ thêm đường chéo AC, cắt EF ở I, rồi áp dụng hệ quả định lí Ta-lét vào các tam giác ADC và CAB.

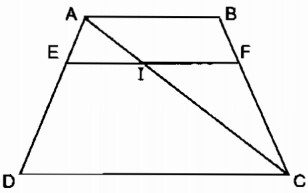
Kẻ đường chéo AC cắt EF tại I.
Trong tam giác AEC, ta có: EI // CD
Suy ra: \({{AE} \over {AD}} = {{EI} \over {CD}}\) (Hệ quả định lí Ta-lét )
Suy ra: \(EI = {{AE} \over {AD}}.CD\) (1)
Lại có: \({{AE} \over {ED}} = {p \over q}\) (gt)
Suy ra: \({{AE} \over {AE + ED}} = {p \over {p + q}}\)
Suy ra: \({{AE} \over {AD}} = {p \over {p + q}}\) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \(EI = {p \over {p + d}}.CD\)
Trong tam giác ABC, ta có: IF // AB
Suy ra: \({{BF} \over {FC}} = {{AI} \over {IC}}\) (Định lí Ta-lét ) (3)
Trong tam giác ADC, ta có: EI // CD
Suy ra: \({{AE} \over {ED}} = {{AI} \over {IC}}\) (Định lí Ta-lét ) (4)
Từ (3) và (4) suy ra: \({{BF} \over {FC}} = {{AE} \over {ED}} = {p \over q}\)
Trong tam giác ABC, ta có: IF // BC
Suy ra: \({{IF} \over {AB}} = {{CF} \over {CB}}\) (Hệ quả của định lí Ta-lét)
Suy ra: \(IF = {{CF} \over {CB}}.AB\) (5)
Ta có: \({{BF} \over {CF}} = {p \over q}\) (cmt)
Suy ra: \({{CF} \over {BF}} = {q \over p} \Rightarrow {{CF} \over {CF + BF}} = {q \over {p + q}} \Rightarrow {{CF} \over {CB}} = {q \over {p + q}}\) (6)
Từ (5) và (6) suy ra: \(IF = {q \over {p + q}}.AB\)
Vậy: \(EF = EI + {\rm I}F = {p \over {p + q}}.CD + {q \over {p + d}}.AB = {{p.CD + q.AB} \over {p + q}}\)
