Câu 116 trang 94 Sách bài tập (SBT) Toán 8 tập 1: Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD....

Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính các độ dài AD, AB (làm tròn đến hàng đơn vị).

Giải:                                                                   

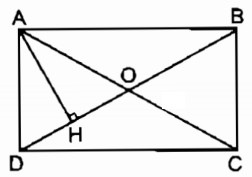
Ta có: DB = HD + HB = 2 + 6 = 8(cm)

AC = DB (tính chất hình chữ nhật)

OA = OB = OC = OD = \({1 \over 2}\)BD = 4(cm)

OD = OH + HD

⇒ OH = OD – HD = 4 – 2 = 2(cm)

AH ⊥ OD có HO = HD = 2(cm)

Suy ra: ∆ ADO cân tại A

⇒ AD = AO = 4(cm)

Trong tam giác vuông ABD có \(\widehat {BAD} = {90^0}\)

\(B{D^2} = A{B^2} + A{D^2}\) (định lý Pi-ta-go) \( \Rightarrow A{B^2} = B{D^2} - A{D^2}\)

\(AB = \sqrt {B{D^2} - A{D^2}}  = \sqrt {{8^2} - {4^2}}  = \sqrt {48}  \approx 7\) (cm).