Giải: . Câu 118 trang 94 Sách bài tập (SBT) Toán 8 tập 1 - Bài 9. Hình chữ nhật
Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
Giải:
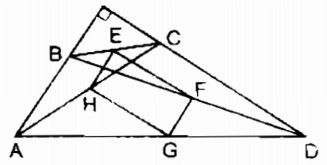
Trong ∆ BCD ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
nên EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF= \({1 \over 2}\)CD (1)
Trong ∆ ACD ta có:
H là trung điểm của AC (gt)
Advertisements (Quảng cáo)
G là trung điểm của AD (gt)
nên HG là đường trung bình của ∆ ACD
⇒ HG // AC và HG = \({1 \over 2}\)AC (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD(gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay \(\widehat {FEH} = {90^0}\)
Vậy hình bình hành EFGH là hình chữ nhật.
