Advertisements (Quảng cáo)
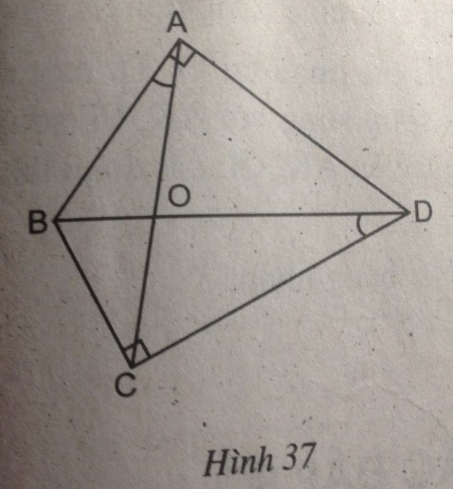
Tứ giác ABCD có hai góc vuông tại đỉnh A và C, hai đường chéo AC và BD cắt nhau tại O, \(\widehat {BAO} = \widehat {BDC}\) (h.37)
Chứng minh:
a. ∆ ABO đồng dạng ∆ DCO
b. ∆ BCO đồng dạng ∆ ADO
Giải:
(hình 37 trang 97 sbt)
a. Xét ∆ABO và ∆ DCO, ta có:
\(\widehat {BAO} = \widehat {BDC}\) (gt)
hay \(\widehat {BAO} = \widehat {ODC}\)
\(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)
Vậy ∆ ABO đồng dạng ∆ DCO (g.g)
b. Vì ∆ ABO đồng dạng ∆ DCO nên:
\({\widehat B_1} = {\widehat C_1}\) (1)
Mà \({\widehat C_1} + {\widehat C_2} = \widehat {BCD} = 90^\circ \) (2)
Trong tam giác ABD, ta có: \(\widehat A = 90^\circ \)
Suy ra: \({\widehat B_1} + {\widehat D_2} = 90^\circ \) (3)
Từ (1) , (2) và (3) suy ra : \({\widehat C_2} = {\widehat D_2}\)
Xét ∆ BCO và ∆ ADO, ta có:
\({\widehat C_2} = {\widehat D_2}\) (chứng minh trên )
\(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)
Vậy ∆ BOC đồng dạng ∆ ADO (g.g)