Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH. Câu 55 trang 98 Sách bài tập (SBT) Toán 8 tập 2 - Ôn tập chương III - Tam giác đồng dạng
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH
Giải:
(hình trang 121 sgbt)
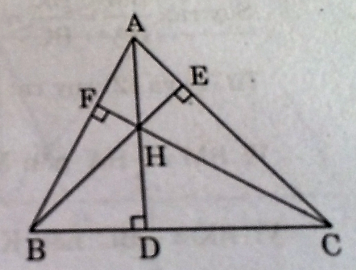
Xét ∆ AFH và ∆ CDH, ta có:
\(\widehat {AFH} = \widehat {CDH} = 90^\circ \)
\(\widehat {AHF} = \widehat {CHD}\) (đối đỉnh)
Suy ra: ∆ AFH đồng dạng ∆ CDH (g.g)
Suy ra: \({{AH} \over {CH}} = {{FH} \over {DH}}\)
Advertisements (Quảng cáo)
Suy ra: AH.DH = CH.FH (1)
Xét ∆ AEH và ∆ BDH, ta có:
\(\widehat {AEH} = \widehat {BDH} = 90^\circ \)
\(\widehat {AHE} = \widehat {BHD}\) (đối đỉnh)
Suy ra: ∆ AEH đồng dạng ∆ BDH (g.g)
Suy ra: \({{AH} \over {BH}} = {{EH} \over {DH}}\)
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.