Tính độ dài x, y của các đoạn thẳng NC và BC.. Câu 8 trang 84 Sách bài tập (SBT) Toán 8 tập 2 - Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
Hình 7 cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC và BC.
Giải:
(xem hình 7)
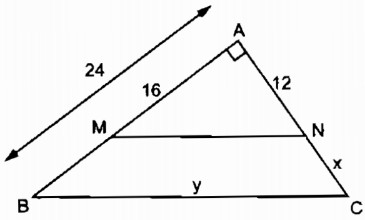
Trong ∆ ABC ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {AC}}\) (định lí Ta-lét)
Suy ra: \(AC = {{AB.AN} \over {AM}} = {{24.12} \over {16}} = 18\) (cm)
Advertisements (Quảng cáo)
Vậy: NC = AC – AN = 18 – 12 = 6 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
\(\eqalign{ & M{N^2} = A{M^2} + A{N^2} = {16^2} + {12^2} = 400 \cr & MN = 20(cm) \cr} \)
Trong ∆ABC, ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{MN} \over {BC}}\) (hệ quả định lí Ta-lét)
Vậy: \(BC = {{MN.AB} \over {AM}} = {{20.24} \over {16}} = 30\) (cm)