
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm tính chia:
a) \((8x + 12 - 4{x^2}):(x - 3)\) ;
b) \((12x - 10{x^2} + 3{x^3} - 8):(x - 2)\) ;
c) \((7{x^2} + {x^3} + 12x - 6):({x^2} + 4x - 2)\) ;
d) \((2{x^2} + 2x - 5{x^3} + 2{x^4} - 1):( - x + {x^2} + 1)\).

a) Sắp xếp theo lũy thừa giảm dần của biến: \(8x + 12 - 4{x^2} = - 4{x^2} + 8x + 12\)
Làm phép chia:
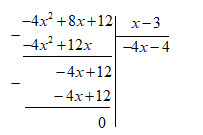
Vậy \(\left( {8x + 12 - 4{x^2}} \right):\left( {x - 3} \right) = - 4x - 4\)
b) Sắp xếp theo lũy thừa giảm dần của biến:
\(12 - 10{x^2} + 3{x^3} - 8 = 3{x^3} - 10{x^2} + 12x - 8\)
Advertisements (Quảng cáo)
Làm phép chia
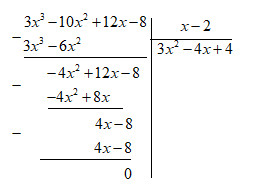
Vậy \(\left( {12x - 10{x^2} + 3{x^3} - 8} \right):\left( {x - 2} \right) = 3{x^2} - 4x + 4\)
c) Sắp xếp theo lũy thừa giảm dần của biến: \(7{x^2} + {x^3} + 12x - 6 = {x^3} + 7{x^2} + 12x - 6\)
Làm phép chia:
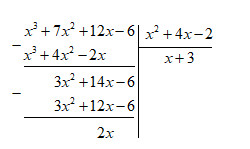
Vậy \(\left( {7{x^2} + {x^3} + 12x - 6} \right):\left( {{x^2} + 4x - 2} \right) = \left( {x + 3} \right)\) (dư 2x)
d) Sắp xếp theo lũy thừa giảm dần của biến:
\(\eqalign{ & 2{x^2} + 2x - 5{x^3} + 2{x^4} - 1 = 2{x^4} - 5{x^3} + 2{x^2} + 2x - 1 \cr & - x + {x^2} + 1 = {x^2} - x + 1 \cr} \)
Làm phép chia:
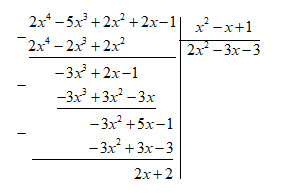
Vậy \(\left( {2{x^2} + 2x - 5{x^3} + 2{x^4} - 1} \right):\left( { - x + {x^2} + 1} \right) = 2{x^2} - 3x - 3\) (dư \(2x + 2\))
